CHAPTER 1 LESSON 6

Before you begin the lesson, take the quiz.

CLICK HERE for the quiz.

Your assignment is to read the notes below and answer the questions that follow.

DIMENSIONAL ANALYSIS

You will recall from earlier lessons that a system of measurement is based on a few selected physical quantities—such as length, mass, time, and temperature—that are measured in arbitrary units. All other quantities are derived from the fundamental quantities and are measured in derived units. Speed (or velocity) is a derived quantity. The average speed of a moving object is defined as the ratio of the distance (length) traveled to the elapsed time of travel.

speed = length = l

time t

Suppose an object travels 576 m in 20.0 s. Its average speed will be

speed = l = 576 m = 28.8 m/s

t 20.0 s

Note: Speed is expressed in dimensions of length/time.

Based on the definition of speed, its dimensions are length/time, or l/t. Observe that the dimensions of speed are also specified in terms of the derived unit m/s. Speed can be expressed in any derived unit that represents its dimensions of length/time. Speed cannot be expressed in any derived unit that does not represent its dimensions of length/time. This concept is fundamental in computations involving the dimensions of physical quantities.

A measurement is expressed as a significant number of some kind of dimensional unit: 12.5 g, 6.72 cm, 10.0 s, 42.1°C, 0.09 g/L, 28.8 m/s. For a mathematical equation to represent the correct solution to a problem, the equation must be dimensionally correct. That is, both sides of the equation must have the same dimensions.

For example, density is defined as the ratio of mass/ volume and has the dimensions of mass/length³. The dimensional unit can be g/cm³. If,

D = m then, g = g

V cm³ cm³

m = D x V then, g = g x cm³ and g = g

cm³

V = m then, cm³ = g

D g/cm³

or, cm³ = g x cm³ and cm³ = cm³

g

Note that terms to both numerator and denominator are “canceled” by dividing both by the common term.

Dimensional analysis is a systematic way of solving numerical problems by the conversion of units.  Frequently, your data will be recorded in one unit, but it will be necessary to do the calculation using a different unit of measurement.  In the second example above, we are given cm³ and we need grams. So we will use dimensional analysis to be able to cancel the cm³ leaving grams. Likewise, in the third example, we want to cancel the grams and end up with cm³. Thus dimensional analysis allows us that step.

This means you should multiply the number you wish to convert by a conversion factor to produce a result in the desired unit.

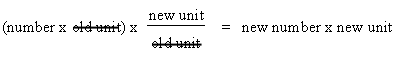
This way, the units in the denominator cancel the units of the original data, leaving the desired units.

Observe that dimensional units common to both numerators and denominators are "canceled" and removed from the expressions in the same familiar way as numerical factors.
Only identical units cancel, as the above operations illustrate. If mass is given in gram units in the numerator of an expression and in kilogram units in the denominator, the units do not cancel directly. For the mass units to cancel, either the measurement in grams must be converted to kilograms, or the measurement in kilograms must be converted to grams. A valid conversion factor that can be introduced into the expression for the purpose of making the desired unit conversion is needed.
Metric units are related as powers of 10 by the system of prefixes. One kilogram is exactly one thousand grams; one centimeter is exactly one one-hundredth meter; one second is exactly one thousand milliseconds. Such a unit relationship can be expressed as a fraction and inserted into an equation as a con-version factor. The form of this conversion factor must allow for the cancellation of the unit to be converted and the retention of the unit required.

Suppose a length / is measured to three significant figures as 1.30 m. How is / expressed in centimeters? By definition, 1 m is exactly 100 cm. A conversion factor with the cm unit in the numerator (unit required) and the m unit in the denominator (unit to be canceled) can be assembled.

In this example, we are given a measurement of 1.30 m. And we want to put the answer in cm. We would use the dimensional analysis.

_
correct l = 1.30 m x 100 cm = 130 cm
m

Note we used the relationship of 1 m to 100 cm. This enabled us to set up the problem so we could cancel the meters and end up with cm.

-
The result, 130 cm, remains precise to three significant figures.

Had the conversion factor been assembled in the inverted form, the meter units would not cancel, the answer unit would not be in centimeters, and the numerical result would not be a correct answer.

(incorrect) / = 1.30 m x m = 0.0130 m²

100 cm cm

Compare these two examples. Both forms of the conversion factor are valid expressions. The second form, m/100 cm, however, is the conversion factor for converting centimeters to meters. Observe that

m x cm = cm and cm x m = m
m cm

The conversion factor used in the first (correct) example not only yields the intended unit in the answer hut also sets up the arithmetic computation that gives the correct numerical answer.

These simple examples of the use of conversion factors reveal an important strategy for solving problems involving measurements and their dimensional units. In any numerical equation, the units associated with the various quantities are treated algebraically and are canceled, combined, etc., just like factors in the equation.

When the numerical expression for the solution to a problem has been assembled, the units in the expression should be "solved" for the answer unit before the arithmetic is done. If the answer unit is dimensionally correct for the physical quantity required, such as g/cm³ for density or m/s for speed, this

indicates that the arithmetic computation should yield the correct numerical answer. On the other hand, unit operations that yield an incorrect answer unit signal that the expression is incorrect and cannot give a correct answer to the problem.

This first unit-operations step is a simple and rapid analysis of the dimensional character of the solution setup for the problem. It is the key step in the problem-solving technique called dimensional analysis. This technique is often called the factor-label method. It is the method used in this course. Later, the factor-label will be extended to include chemical formulas in the unit-operations step of problem solving.

Remember, the factor-label method uses unit operations to set up the arithmetic in problem solutions.

The following Sample Problems illustrate this factor-label method.

Problem 1
A chemistry student was asked to determine the density of an irregularly shaped sample of lead, but was not supplied with any measurement data.

Solution:
The student measured the mass of the lead on a "centigram" balance as 49.33 g. Recalling from General Science that a solid displaces its own volume in a liquid, the student immersed the lead in water contained in a cylinder graduated in 0.1-mL divisions. The sample displaced 4.35 mL of water, the 0.05 mL being estimated.
Because the volume of a solid is normally expressed in cubic measure, the measured volume was converted to cubic centimeters.

Since 1 mL = 1 cm³

4.35 mL x 1 cm³ = 4.35 cm³
mL

Again, we wanted the answer in cm³, but we were given mL in the problem. So we used the conversion factor of 1 mL being equal to 1 cm³ This allowed us to set up the problem so that we could cancel the mL’s and get the cm³

By definition: D = m, = 49.33 g = 11.34 g/cm³
V 4.35 cm³

The multiplication/division rule for significant figures indicates an answer to 3 significant figures in this computation. Therefore, the result is rounded off to 11.3 g/cm³.

A more efficient solution setup for this problem is

D = m, = 49.33 g = 11.3 g/cm³
4.35 mL x 1 cm³/mL

Problem 2 _
Determine the concentration of table salt (sodium chloride) in grams of salt per gram of solution, when 400 mg
_
of the salt is dissolved in 100 mL of water at 60 °C.

Solution:
The problem requires that the solution concentration be expressed in grams of salt per gram of solution. Therefore, the solution concentration is derived from the ratio: mass salt/mass solution. The mass of the solution is the sum of the mass of salt dissolved and the mass of water used. The volume of water at 60 °C is , known, but its mass is required. Density relates the mass and volume of a material. The density of water at 60 °C is listed in Appendix (Density of Water Chart—Click here). Locate this table and verify that the density of water at 60 °C is 0.983 g/mL.

By definition: D = m
V

Solving for m: m = D x V

_
Substituting: m = 0.983 g x 100 mL water = 98.3 g water
mL

Observe that the unit operations yield the correct answer unit for the mass of water.

The mass of salt is given in milligrams. As milligrams and grams cannot be added, milligrams of salt must be converted to grams.

By definition: 1 mg = 0.001 g

_
400 mg salt x 0.001 g = 0.400 g salt

mg

Observe that the factor 0.001 g/mg is exact.

mass of solution = 0.400 g salt + 98.3 g

water mass of solution = 98.7 g solution

solution concentration = mass salt = 0.400 g

mass solution 98.7 g solution

solution concentration = 0.00405 g salt/g solution

Here is another way to do the same problem.

In this example, the complete solution setup is developed in literal terms (without number values) as an algebraic equation. Measurement values are then substituted, and the indicated unit operations are performed to verify the correct answer unit—grams salt per gram solution. It is an efficient method and a productive approach to the problem-solving process.

solution concentration = mass salt = mass solution = m_s

mass solution m_soln

But, m_soln = mass salt + mass water = m_s + m_w

And, m_w = density of water x volume of water = D_w x V_w

Therefore, soln conc = m_s

[m_s + (D_w x V_w)]_soln

_
soln conc = _ 400 mg salt x 0.001 g/mg _

(400 mg x 0.001 g.mg + 0.983 g/mL x 100 mL)_soln

soln conc = 0.400 g salt = 0.400 g salt

(0.400 g + 98.3 g) soln 98.7 g soln

soln cone = 0.00405 g salt/g soln

PRACTICE PROBLEMS

1. Using a platform balance, the mass of an irregular block of iron is found to be 280.2 g. The iron was immersed in water and found to displace 35.6 mL of the water. Determine the density of the iron.

2. Determine the concentration of a solution in grams of salt per gram of solution when the solution is prepared by dissolving 10.2 g of a certain salt in 500 mL of water at 50 °C.

Click here to see solution to problems