CHAPTER 2 LESSON 4

If you need to contact your math teacher for additional help, stop by the chatroom or use the Math Response Form.

CLICK HERE FOR RESPONSE BOX PAGE

First take Quiz and then return to this Lesson. Click here for Quiz

"PROOFS AND MORE COMPLEX FIGURES"

After the quiz, In your book, page 57, "Proofs and More Complex Figures"

This section illustrates how we can use the Subtraction Property of Equality to help us in solving proofs.

RECALL the

Subtraction Property of Equality: if a = b, then a - c = b - c

Please note in your textbook on page 57,

what can happen with the Segment Addition Postulate and Angle Addition Postulate.

Remember that the segment addition postulate stated that we can add the segments together to create a larger segment and that the angle addition postulate stated that we can add adjacent angles together to create a larger angle. Note these two in your book !!

Given: AB with C on AB and Given: Ð ACB, with ray CD in the interior section of Ð ACB

Now with the Subtraction Property we can do more than that.

For example:

we can add segments together to create a larger segment AC + CB = AB

but if we have to isolate a smaller portion of the line segment
we can subtract--

example:

AC = AB - CB or CB = AB - AC

So this adds to our ability to solve proofs. The same is true for angles

Note in the book the angle addition postulate. But if we have to isolate a smaller angle we can use the subtraction property of equality to do this.

Another example:

Remember the steps that need to be taken to write a proof. ?
What has to be proven? Then think of a plan to accomplish this.

1. What do they want you to prove? that the m Ð 6 is equal to the m Ð 8. 2. How are we going to prove this?

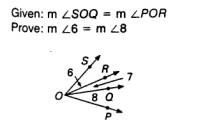
Look at the Given. The m Ð SOQ is equal to the m Ð POR. Now what angles are a part of Ð SOQ?? Ð 6 and 7. What angles are a part of Ð POR? Ð 7 and 8.

This is the angle addition postulate because we are adding Ð 's 6 and 7 together to get Ð SOQ and adding Ð 's7 and 8 to get Ð POR

But we have to get Ð6 to be equal to Ð8.
So let's take the first Ð SOQ and subtract Ð 7 from it, leaving Ð 6 and then take Ð POR and subtract 7, leaving Ð 8 from it.
Therefore because the given told us that the larger Ð 's SOQ and POR were equal, we can substitute thereby giving us the fact that Ð 6 is equal to Ð 8.

Now let's write the proof. J Please note ***** this information is not required for the proof. I have supplied it so that you can see why I used that step.

STATEMENT REASON

1. m Ð SOQ = m Ð POR Given

******(Prove that you have two angles creating a larger angle)
2. m Ð 6 + m Ð 7 = m Ð SOQ;
m Ð 8 + m Ð 7 = m Ð POR Angle Addition Postulate

********(Now subtract one angle from the larger one

3. m Ð SOQ - m Ð7 = m Ð6;
m Ð POR - m Ð 7= m Ð 8 Subtraction property of equality

4. \ m Ð 6 = m Ð 8 Substitution

\ symbol for Therefore

Look over Example 1 in your book on page 57. The only above is much like that one.

Now look at Example 2 on page 58

Again go through the process to solve a proof. First, What you do they want you to do?
Answer: Prove that AB @ CD.

Second, what have they provided you in the given? That on a line segment AC @ BD. The problem is that they have given you a part of the line segment that is not needed, namely BC.

Third, develop a plan to solve the proof. What do you know about line segments? I know that if I add line segments together that I can create a larger segment. AB + BC = AC

___________________________
A B C AB + BC = AC Angle Addition Postulate

but in this case, I have to get rid of line segment BC. So I will subtract BC from AC to get AB and again subtract BC from BD to get CD. Look at the given again. They give us that AC @ BD.
SEE BELOW

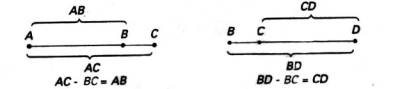
Then begin to write the proof in a two categories: Statement and Reason

1. AC @ BD (AC= BD) Given
2. AB + BC = AC; BC + CD = BD Segment Addition Postulate
3. AC - BC = AB; BD - BC = CD Subtraction Property of Equality
4.\ AB = CD ( AB @ CD) Substituition

Now look at the last example, #3 on page 58.

First, what do they want you to do? Prove that the measure Ð 1 and the measure Ð 3 is 90. Second, Look at the Given. What do they give you? That ray BA and ray BC are perpendicular and ray BC bisects Ð B (Read the angle as the middle letter-example DBE the angle is located at point B)

Now what do you know about these things? First, perpendicular lines. We know that they create 90 right angles (Theorem 1.1) You also know that COMPLEMENTARY ANGLES ARE ALSO 90. Remember complementary angles are 2 angles equaling 90 degrees.

What do you know about angle bisectors? That they divide the angle into 2 equal sections.

Now put this to work on the proof.!!!!!!!

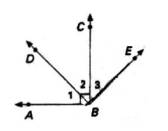
Notice that in the given or in the picture that angles 1 and 2 are complementary. But they want you to prove that angles 1 and 3 are complementary. But that is ok, because we know from the given that there is a angle bisector and that means that angles 2 and 3 are equal to each other. Therefore, we can switch or substitute 2 and 3 and create the fact that angles 1 and 3 are equal to 90.

Now you have the plan, let's write the proof

1. Ray BA ^ Ray BC Given
2. m Ð 1 + m Ð 2 = 90 If outer rays of acute adjacent angles are
perpendicular, then the sum of the angles is 90
3. Ray BC bisects Ð DBE Given
4. m Ð 3 = m Ð 2 Definition of angle bisector
5. \ m Ð 1 + m Ð 3 = 90 Substitution

Just a couple of things

When you submit your answers to the problems, you are not going to be able to use a symbol for the word (example perpendicular ^ ) you will have to write out the word in your statement.

For example in number 1 above, you would have to write

1. Ray BA is perpendicular to Ray BC.

Now let's begin to work. Page 60-61. Work on problems 4-14 even only.

Student's First & Last Name:

Please number your answers

The submit button has been disengaged

BACK TO SAMPLE PAGE